実はこの光速度不変の原理を採用するとたちまち奇妙なことが起こります.まずはその例をお見せしましょう.
真夜中,とある駅のプラットホームにあなたは立っています.あなたは正確な時計を持っています.今あなたの左手から秒速10万キロの一定速度で走る長さ20万キロメートルの1両の電車がやってきました(そんな電車ありえないですが,話をわかりやすくするため,そういう電車が存在することにします.こういうのを思考実験といいます).電車のちょうど真ん中に一人の人物が立っていて,彼(彼女)の頭上に電球がぶら下がっています.その人物もあなたと寸時も違わない時計を持っています.そして電車の両端にもあなた方と同じ時計が設置してあるものとします(絵1). |
|
|

絵1 |
|
|
|
今,電車の中央があなたの場所に来た瞬間,車内中央の電球が一瞬点灯しました.車内の人物からはこの光はどう見えるでしょう.
光速度不変の原理に従えば,車内の電球から発せられた光は秒速30万キロで電車の前後両方に広がります.その人物は電車の中央に立っていますから,彼(彼女)から見ると点灯の0.333…秒後(時間=距離÷速さなので)に電車の前後端に光は同時に到着します(絵2). |
|
|
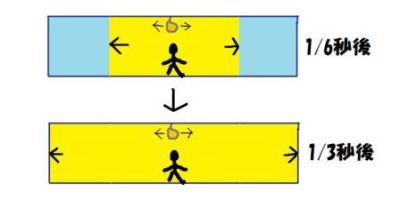
絵2 |
|
|
|
今ここで光が電車の前端に到達することを事件A,後端に到達することを事件Bとしますと,電車の人物から見た事件Aと事件Bは同時刻に起こるように見えます.ここまではなんの問題もないはずです.
さて一方あなたから見た場合はどうでしょう.あなたから見た時も光速度不変の原理は成立しますから,電球が光った瞬間から光は電車の前後方向に,あなたから見てどちらも秒速30万キロで進んでいきます.ところがあなたから見た電車は動いていますから,仮に0.333…秒経過したとしても,電車の進行方向ではまだ光は前端に届いていません.しかし電車の反対方向ではとっくに端に到達していることになります(絵3). |
|
|
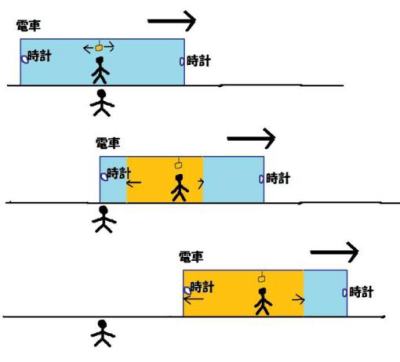
絵3 |
|
|
|
あなたから見ると事件Aと事件Bは同時刻には起こりません.すなわち同じ現象を観察しているにも関わらず,電車の中の人から見ると同時刻に起こるのに,プラットホームからは同時刻には見えないのです.これは矛盾ではないのでしょうか.
しかしアインシュタインはこれを矛盾と考えませんでした.人によって同時刻に見えようが見えまいが構わない,お互いにそれで困ることはないのだからという彼のスタンスです.これを同時刻の相対性といいます.同時刻という概念も絶対的なものではなく,それぞれの観測者(この場合は電車内の人物とプラットホームのあなた)ごとに違うのだということです.えらくムチャクチャな気がしますが,たしかにプラットホームのあなたの前を通過して行った電車は,二度とあなたの前に現れることはないのですからそうかもしれません(電車は等速直線運動をしているので永遠に遠ざかっていく).
じゃあ,電車が途中で向きを変えて戻ってきたらどうなんだと言いたくなるかもしれません.その場合は電車は向きを変えるために加速度運動を必要としますから,今回の特殊相対性理論では扱えない話になるので,別に考えればいいのです.
ひどいたとえでしたが,アインシュタインのいいたいことは,それまで自分たちが絶対普遍のものと信じていた時間というものが,実は絶対的なものではないのだということです.時間は誰から見ても同じリズムで時を刻んでいると私たちは思っています.しかしそれが実は真実ではないというのがアインシュタインの意見なのです.
注) 現実的な言い方をすると,事件Aと事件Bがプラットホームにいる人の目に届くのに要する時間は異なります.事件Aの映像が届くのに要する時間が長いわけですから同時刻でないことも実は不思議でないわけです. |
|
|