2008年1月にニュース上で極めて興味深い記事が出ていた.
「三角形は一つの曲線と二つの曲線に囲まれる」??あきれた教師、分限免職
記事によるとこの教師は,色々と教える内容に問題があったのだそうだが,その代表例として表題の「三角形は…」を取り上げたものらしい.
確かに小中学校では,「三角形は3本の直線によって構成されていて,その内角の和は180度である」と教えられる.小学校で使った三角定規を思い出せば,直感的に納得できる事だろう.しかし常識と真実は必ずしもイコールではない.三角形が3本の直線から構成され,内角の和が180度になるというのは,ユークリッド幾何学の世界においてのことだからである.
ユークリッド幾何学は古代ギリシャのエウクレイデス(英語読みでユークリッド)が完成させた幾何学の体系で,基本的に平面および歪みのない空間を対象とした幾何学である.平面上に書かれた三角形は確かに3本の直線から構成されているし,平行線は決して交わることはない.この意味からいえば件の教師の授業は明らかにおかしいといえる.
しかしこの世の中はすべて平面で歪みのない空間というわけではなく,時としてユークリッド幾何学が通用しない世界も存在するのである.その代表例が球面である.私達も知っている地球儀をよく見ると,経線というのがある.北極と南極を結ぶ直線で,ロンドンのグリニッジ天文台を 通る線を0度として以東を東経,以西を西経としている. |
|
| 地球儀上には無数の経線が引けるのであるが,経線は全て直線である.しかし経度の異なる2本の経線は必ず北極点と南極点という2点で交わっている.ユークリッド幾何学の世界では,これは絶対にありえない話である(ユークリッド幾何学では,2本の直線は平行でなければ,必ず1点のみで交わる).また地球儀上では2本の経線で囲まれた空間が存在するのだが,2本の直線で囲まれた空間が存在するとは,すな わち2角形が存在するということであり,これまたユークリッド幾何学ではありえない話である(二角形なんてだれも聞いたことないですよね). |
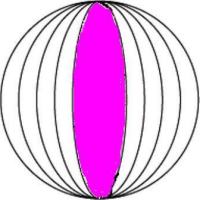
経線は平行線だが2点で交わる |
|
|
ただありえないからといって,存在を否定することはできず(「あるんだから仕方がない!」という感じ),結局これは,この世にはユークリッド幾何学が適応できない空間が存在するということである(なんだか四次元世界みたいだが,四次元と違うのは,その存在を我々も実感できるという点).これが非ユークリッド幾何学と呼ばれるものであり,先に述べた地球儀の話も,非ユークリッド幾何学の1種である(球面幾何学).
|
|
球面幾何学では,直線とは大円(交差する平面が球の中心を通る線,簡単に言えば経線や赤道)のことであり,2本の直線は必ず2点で交わる.しかも任意に書いた三角形の内角の和は180度以上になる.そこで球面上に書いた三角形を切り出してみると,ほら,なんだか曲線みたいに見えますよね(厳密に言えば,球面上に書いた三角形の1辺も直線であることに変わりはないんですが,視覚的には曲線に見える).
|
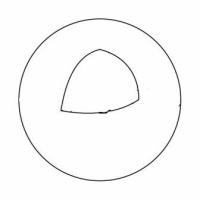
球面上の三角形は丸みを帯びて見える |
|
|
私は件の教師が言ったという,「三角形は一つの曲線と…」の話は,この非ユークリッド幾何学のことが念頭にあったんじゃないかと勝手に思ったのでした(んなわけないか 笑).
注) 実際には平面だろうと曲面だろうと,三角形の辺は全て直線です.上記の絵はあくまでも”曲線に見える”だけですので誤解のなきように願います. |
|